Monday, October 6, 2014
Network map of the Ukraine
There is a tolerably well-known exercise for illustrating the graphical superiority of a Non-Metric Multidimensional Scaling (NMDS) ordination over a Principal Components Analysis (PCS) ordination. The latter is often subject to distortions, so that the relative positions in the scatter-plot of points do not represent the original measured distances between those points (see the post Distortions and artifacts in Principal Components Analysis analysis of genome data). The exercise consists of using the geographical distances between locations on a map as the input distances to the analyses. The NMDS ordination will re-create the map quite accurately while the PCA ordination will usually not do so.
Some time ago I had the idea of doing this same exercise using a data-display network. Unfortunately, I was beaten to it by Barbara Holland (2013. The rise of statistical phylogenetics. Australian and New Zealand Journal of Statistics 55: 205-220). I will go ahead, anyway, disappointed though I am.
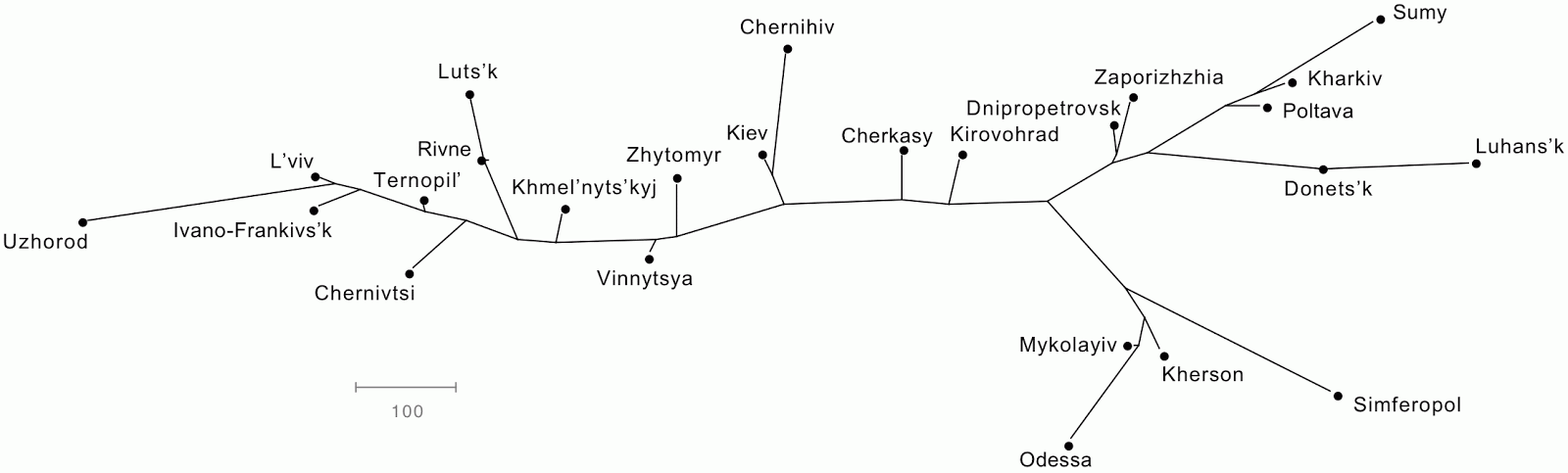
I have chosen the Ukraine as my map. The road distances between 25 of the cities were taken from Ukraine Connections (the same data occur on several other sites, as well).
The geographical data were processed in SplitsTree to produce both a Neighbor-Joining tree and a NeighborNet network.
If these techniques are to be effective as data displays, then the positions of the cities in the line graphs should be approximately the same as those in the map. This is, indeed, roughly so, although I had to spend some time manually adjusting the branch angles in the tree (for the best match). The two graphs are more rectangular in overall shape than is the Ukraine, which is somewhat closer to a square, but the relative locations of the points in the graphs do tell you where to look for the cities on the map.
However, the network is the better of the two representations on two grounds. First, the points are constrained to certain locations, and do not need manual adjustment. Second, the network more accurately gives a sense that these are road distances, and there are multiple roads from one city to another — the tree incorrectly implies that there is only one way to get between the cities.
Labels:
EDA,
Map,
Splits graph
Subscribe to:
Post Comments (Atom)



No comments:
Post a Comment